|
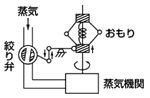
Q1-1.誤信号が発生するのは機構上、仕方がないのか? Q1-2.ひずみゲージは何のために取り付けてあるのか? Q1-3.ひずみ感度の小さいセンサを用いることによるデメリットは無いのか? Q1-4.異常な振動挙動に時間差があるのはなぜか? Q1-5.計測ラインによって温度が上がるのはなぜか? Q1-6.トリップとは具体的にどういうことか? Q1-7.ノイズは頻繁にのるのか? Q1-8.チャージアンプの飽和現象とはどういう現象のことか? Q1-9.圧電素子が、ノイズでひろう電圧と振動による電圧の差はどの程度か? Q1-10.軸受の種類によって振動の周波数領域はどのくらい違うか? Q1-11.対応できる周波数領域の異なるピックアップはないのか? Q1-12.このような作業はよくおこなわれるのか? Q1-13.測定できる最大周波数はどのくらいか? Q2-1.回転機械の他の振動は、どんな振動があるか? Q2-2.偏心のない回転体は作れないのか? Q2-3.危険速度とはどういった状況の速度のことをさすのか? Q2-4.おもりを付ける位置はどのようにして決めるのか? Q2-5.影響係数法とはなにか? Q2-6.JIS規格はどのようにして決まったのか? Q2-7.剛性、準弾性、弾性ロータはどのような場で用いられているか? Q2-8.剛性、準弾性、弾性ロータの長所、短所は? Q2-9.振動感度を低くするにはどうすればよいか? Q2-10.設計計算の精度は、実測と比べどの程度か? Q3-1.管内波動では、何が振動するのか? Q3-2.管端が閉鎖と開放で反射は変わるのか? Q3-3.流体系では何が振動するか? Q3-4.反共振とはどのような現象か? Q3-5.ウォータハンマ、エアハンマを弱めるにはどうすればよいか? Q3-6.フィードバックの具体例には、どのようなものがあるか? Q3-7.管路系の固有振動数を調べるにはどうすればよいか? Q3-8.共振現象は設計の段階から考慮できないのか? Q3-9.130dBとはどのくらいの音か? Q3-10.発熱作用はどう振動に影響するのか? Q3-11.ヘルムホルツ共鳴器はどういう役割を果たしたのか? Q4-1.建物の等価質量はいつも1/4なのか? Q4-2.等価質量を求める方法はあるか? Q4-3.動吸振器の質量はどのくらいが現実に使われているか? Q4-4.最適調整の値は解析的に求められるか? Q4-5.動吸振器を設計する上の留意点は? Q4-6.ねじり振動の低減にも使えるか? Q4-7.自励振動防止にも使えるか? Q5-1.高速回転機械とは、どれくらいの回転数か? Q5-2.フィールドバランスとは? Q5-3.低負荷の場合にのみオイルホイップが起こるのか? Q5-4.軸受特性を変えてオイルホイップ発生を変えたことの詳細は? Q5-5.原因を判定するキーポイントをどのように適用したか? Q5-6.応急対策として、軸受幅を小さくしたのはなぜか? Q5-7.波形観測のため、振動はどこの部分を測ったのか? Q5-8.ジャーナルの偏心が小さくなるのはなぜか? Q5-9.オイルホイップが起こるのは、危険速度の2倍の回転速度だけか? Q5-10.イナーシャ効果と負荷の関係は? Q5-11.回転数の半分の成分がなぜあるのか? Q5-12.オイルホイップ発生後、回転数をさらに上げるとどうなるか? Q5-13.オイルホイップとオイルホワールの違いは? Q5-14.強制振動の対策はどうするか? Q5-15.プリロード係数とは? Q5-16.2円弧ジャーナル軸受とは? Q5-17.アライメントとは? Q5-18.シムアップとは? Q5-19.なぜNo.2の軸受温度が今までより高くなったのか? Q6-1.時間遅れとは、何の何に対する遅れのことか? Q6-2.接触回転系2はロールではなく、他の接触系が動く場合にも、パターン形成現象は起こるか? Q6-3.最初の変形理由は何か? Q6-4.パターンが生じると機械にどのような影響を及ぼすか? Q6-5.接触力の変動が起きる理由は? Q6-6.上下ロールの変化に違いはあるか? Q6-7.タイヤの多角形摩耗を防ぐにはどのような対策があるか? Q6-8.ドライブロールの回転速度を変化させると振動はどう変化するか? Q6-9.下ワークロールは変形しないのか? Q6-10.多角形穴にしないためにはどうすればいいか? Q7-1. 磁気軸受の磁気吸引力の求め方は? Q7-2. 磁気軸受はどのような機器に使われているか? Q7-3. 磁気軸受の規格はどうなっているか? Q7-4. 磁気軸受の制御について知りたい。 Q7-5. 磁気軸受の磁極の形状はどのようになっているか? Q7-6. 磁気軸受の特徴を知りたい。 Q8-1.設計過程ではどういったチェックが行われるか? Q8-2.フラッタ以外の自励振動の例としては、どういったものがあるか? Q8-3.行きと返りの仕事が違うとはどういうことか? Q8-4.他のフラッタとして失速フラッタはどのようなメカニズムか? Q8-5.微小外乱にはどういったものがあるか? Q8-6.減衰項、慣性項に非対角項がある場合はどうなるか? Q8-7.フラッタのエネルギ考察を理論的に行うとどうなるのか? Q8-8.RouthHurwitzによる方法とはどういう方法か? Q8-9.揚力の発生が少なくなるような流体力学的配慮の例として、どのような方法が挙げられるか? Q9-1.摩擦振動とは? Q9-2.指数関数的に成長する振動とは? Q9-3.なぜ負荷の部分を打撃したか? Q9-4.自励振動と強制振動の特徴は? Q9-5.摩擦は振動の減衰に効くのではないのか? Q9-6.なぜ摩擦による自励振動と判断したのか? Q9-7.摺動部の潤滑は、どのようになっているか? Q9-8.スティックスリップの例としては、どのようなものがあるか? Q9-9.事例の現象がスティックスリップではないと判定したのはなぜか? Q9-10.剛性マトリックスに非対称な項が、自励振動の原因になるのはなぜか? Q9-11.なぜ下降では自励振動が発生し、上昇では発生しないのか? Q10-1.誘導電動機の騒音が最近とくに問題になるのはなぜか? Q10-2.電動機の騒音はどのような原因から発生しているのか? Q10-3.電磁力が加振するメカニズムは? Q10-4.高調波成分とは? Q10-5.高調波成分が騒音の源となる原因は? Q10-6.有限要素法や境界要素法とは何か? Q10-7.実際の騒音はどの程度か? Q10-8.設計段階でシミュレーションはどの程度行われているのか? Q10-9.理想的な設計でのこれら2つの関係はどのようなものか? Q10-10.円環次数とは? Q10-11.リブとは? Q10-12.リブをつけることで得られる効果は? Q1-1 誤信号が発生するのは機構上、仕方がないのか。 A1-1 圧電型加速度ピックアップにかぎらず、どのようなセンサにおいても測定環境条件のなかで誤信号を発生するなど固有の精度上の限界がある。センサ固有の性能や信頼性について取扱説明書でよく知った上で、そのセンサのもつ性能や特徴を活かして使用することが大切である。この事例のようにセンサ取り付け部の剛性の違いからひずみ感度が相違して誤信号が発生しているものと思われる。 Q1-2 ひずみゲージは何のために取り付けてあるのか? A1-2 ひずみゲージは圧電型加速度ピックアップのノイズの種類として測定対象物の振動による変形、すなわち、取り付け面のひずみが発生していないか否かをチェックし、ひずみ感度の影響を調べるためのもので、本来の振動計測では不要のものである。 Q1-3 異常な振動挙動に時間差があるのはなぜか? A1-4 一般に機械の負荷を上げた場合に、振動計を取り付けている部分の局所的な温度が上昇するまでには時間を要する。さらに振動計の温度特性不良の現象とあいまってこのような時間差が発生するものと考えられる。 Q1-5 計測ラインによって温度が上がるのはなぜか? A1-5 計測ラインの設置される機械の場所における雰囲気温度の差異で温度が上がるものと考えられる。 Q1-6 トリップとは具体的にどういうことか? A1-6 機械のある部分に振動などの異常現象が発生する初期段階で異常振動などを検知して、機械の致命的な損傷につながるのを防ぐ目的で、機械を事前に一時的に緊急停止すること。 Q1-7 ノイズは頻繁にのるのか? A1-7 工場のような動力配線が計測ラインの近くにあるような場合には、ノイズが頻繁にのるものとみて対策が必要である。 Q1-8 チャージアンプの飽和現象とはどういう現象のことか? A1-8 負荷の増加に伴って発生した電源ノイズによる電圧がチャージアンプに入り、電圧が飽和となる異常状態のことだと考えられる。 Q1-9 圧電素子が、ノイズでひろう電圧と振動による電圧の差はどの程度か? A1-9 圧電素子そのものの入力と出力の関係を示す直線性はきわめて広範囲だが、加速度ピックアップの構造上、各種のノイズひろう結果となる。電源ノイズの場合には信号以上に大きくなる恐れもあるが、これは異常なので取り除く必要がある。 Q1-10 軸受の種類によって振動の周波数領域はどのくらい違うか? A1-10 ころがり軸受の振動を診断するうえで、着目すべき特徴的な周波数は回転周波数または回転周波数と転動体(玉またはころ)の個数との積に比例する。軸受の種類のほかに運転速度によっても着目すべき周波数は変わる。 Q1-11 対応できる周波数領域の異なるピックアップはないのか? A1-11 標準的な加速度ピックアップの周波数範囲よりも広い、より高性能な加速度ピックアップを使用すれば改善を図ることができる。しかし、この場合でも測定作業の時間的な効率化や測定対象面の都合で加速度ピックアップに探触棒をとりつけることによって測定がおこなわれるため、共振周波数が低下することは避けられない。 Q1-12 このような作業はよくおこなわれるのか? A1-12 メーカー側から市販された加速度ピックアップの周波数特性や、振動測定対象物とピックアップからなる振動特性を、ユーザー側はよく知ることによって今回のような振動測定作業の改善をはかることができる。このような作業はユーザー側の測定上のノウハウとなっている。 Q1-13 測定できる最大周波数はどのくらいか? A1-13 測定できる最大周波数は加速度ピックアップ自体の質量・ばね系の共振周波数によって決まる。一般用のピックアップでは共振周波数範囲は20から30kHzである。また特殊小型ピックアップの場合は180kHzである。これらの共振周波数よりも少し低い範囲で実際の測定はおこなわれる。共振周波数については加速度ピックアップのメーカーの技術革新によって更新されているようである。 Q2-1 回転機械の他の振動は、どんな振動があるか? A2-1
Q2-2 偏心のない回転体は作れないのか? A2-2 加工によって達成できる高精度でも、許される偏心量よりも何倍もあり、どうしても仕上げにつりあわせが必要である。 Q2-3 危険速度とはどういった状況の速度のことをさすのか? A2-3 振動がピークになる回転数で、回転数と固有振動数が一致する回転数のことである。 Q2-4 おもりを付ける位置はどのようにして決めるのか? A2-4 画面5のような計算で実測ベースで求める。 Q2-5 影響係数法とはなにか? A2-5 試しおもりが振動に及ぼす影響とベクトルで求めこれを利用して逆算する。影響計数法に関しては、現在、奥深い知識や研究が進んでいる。 Q2-6 JIS規格はどのようにして決まったのか? A2-6 実績ベースでISOと照らし合わせて決定された。 Q2-7 剛性、準弾性、弾性ロータはどのような場で用いられているか? A2-7 実際のロータを適宜分類したもの。 Q2-8 剛性、準弾性、弾性ロータの長所、短所は? A2-8 回転機械は極限設計になっており、結果として剛性、準弾性、弾性ロータになる。剛性ロータにすると振動はやさしいが性能が悪く、弾性ロータにすると振動は出やすいが性能がよくなる。 Q2-9 振動感度を低くするにはどうすればよいか? A2-9 軸の剛性を上げて減衰の良く効く軸受を使えばよい。 Q2-10 設計計算の精度は、実測と比べどの程度か? A2-10 実績がどれ位あるかに依存するが、うまくやれば±20%位の精度で予測が可能である。 Q3-1 管内波動では、何が振動するのか? A3-1 流体粒子が管長方向に振動する。(一般には流れに重畳して)。振動によって前後の間隔が変化し密度変化あるいは圧力変化が生じる。この変化が波動となって音速で管の前後に伝播する。 Q3-2 管端が閉鎖と開放で反射は変わるのか? A3-2 管端で波は反射するが閉鎖と開放では反射波の位相が異なる。閉鎖端では圧力波は同位相、粒子速度波は逆位相となる(したがって反射端では圧力は2倍、粒子速度は0となる)が、開放端では圧力波は逆位相、粒子速度波は同位相で反射する。 Q3-3 流体系では何が振動するか? A3-3 流体粒子が管長方向に(一般には流れに重畳して)振動する。密度変化や圧力変化も振動する。 Q3-4 反共振とはどのような現象か? A3-4 正弦波で加振したときの応答振幅を周波数応答線図でプロットすると山と谷を繰り返すような曲線になる。山は共振点で谷のところが反共振点である。反共振点は力を加えても振動が生じにくいところである。周波数を変えると振動の節の位置が変わっていくが、反共振点では節のところで加振していることになる。 Q3-5 ウォータハンマ、エアハンマを弱めるにはどうすればよいか? A3-5 弁を緩やかに操作するなど外乱を小さくすることが大切である。ショックを吸収するための緩衝装置たとえば、管路系ではアキュームレータを設置することも有効である。 Q3-6 フィードバックの具体例には、どのようなものがあるか? A3-6 機械やプラント機器などではフィードバック制御がよく使われている。これは制御したい量と目標値の差を検出しその差が小さくなるよう操作量を変更するものである。たとえば温度を一定に保ちたい場合、時々刻々の温度を測定し目標値よりも高ければヒータの出力を下げ、低ければ出力を上げるような制御を行う。結果をみてそれに応じて元の操作量を調節することからフィードバックという言葉が使われている。 Q3-7 管路系の固有振動数を調べるにはどうすればよいか? A3-7 計算と実験を二つの方法がある。計算では画面8の方法が利用できる。 実験では自由振動を発生させて振動数を読み取るか、正弦波加振して共振させ共振の周波数を読み取ることになる。空気管路ではスピーカを用いた加振実験がよく行われる。 Q3-8 共振現象は設計の段階から考慮できないのか? A3-8 伝達マトリックス法、有限要素法、境界要素法などに基づいて作成されたコンピュータソフトでシミュレーションすれば共振現象を予測することができる。 Q3-9 130dBとはどのくらいの音か? A3-9 ジェット機の離陸時の音をま近に聞くと130dB程度あり、耳が痛くなる。 またガード下での電車通過音は100dB程度である。 Q3-10 発熱作用はどう振動に影響するのか? A3-10 熱が加わると気体は膨張する。発熱変動は気体の体積を変化させ、これが加振源となって振動や音を発生させる。 Q3-11 ヘルムホルツ共鳴器はどういう役割を果たしたのか? A3-11 ヘルムホルツ管の固有振動数を問題になっている振動の周波数に合わせるように調整するとヘルムホルツ管の質量・ばね系が共振を起こした状態になり大きく振動する。そして元の振動系の身代わりになって振動する感じになり本体側の振動が小さくなる。 Q4-1 建物の等価質量はいつも1/4なのか? A4-1 地盤が強く固定支持のときは1/4、極単に柔らかくなると1/3に近づいていく。 Q4-2 等価質量を求める方法はあるか? A4-2 通常の状態で固有振動数 固有振動数  Q4-3 動吸振器の質量はどのくらいが現実に使われているか? A4-3 質量比で 最適調整の値は解析的に求められるか? A4-4 質量比 主振動系固有振動数 固有振動数比 とおいて、次式で与えられる。 Q4-5 動吸振器を設計する上の留意点は? A4-5 できるだけ大きい質量比Rを選ぶ。 動吸振器が振れすぎてばねk2の強度限界を超えないこと。 Q4-6 ねじり振動の低減にも使えるか? A4-6 使える。参照画面の教科書にもあるように、昔からねじり振動防止に回転遠心場の振り子(遠心振り子)が使われている。また、往復形内燃機関にはフードダンパやランチェスターダンパと呼ばれるものも昔から使われている。 Q4-7 自励振動防止にも使えるか? A4-7 使える。機械学会論文集にいくつかの事例が報告されている。 Q5-1 高速回転機械とは、どれくらいの回転数か? A5-1 特に回転数で決まるものではない。普通は、重要な危険速度(ロータの曲げモードの最低次の危険速度)を超えて運転する機械をそう言っている。もちろん、この定義にあてはまらなくても、10,000rpmの機械を高速と言っても、かまわない。 Q5-2 フィールドバランスとは? A5-2 ロータ製造時に、工場でつりあい試験機(バランシングマシン)でつりあわせ(バランシング)するのが通常である。一方、運転時に不つりあいによる振動が大きい場合には、現場で、バランス用の計測器や一般的な振動計を使ったデータに基づいてつりあわせ量を決め、現場で施工して、ふれまわり振動を小さくすることを、フィールドバランスと呼んでいる。 Q5-3 低負荷の場合にのみオイルホイップが起こるのか? A5-3 どの機械でも負荷が小さいとオイルホイップが起こり易い、とはいえない。機械のメカニズムが違えば発生の仕方は異なるのが普通である。一般的に、機械は定常(最大に近い)使用で能力が設定されていて、低負荷では無理をするようなことになっているので、異常が起こり易い。これについては、後述する。 Q5-4 軸受特性を変えてオイルホイップ発生を変えたことの詳細は? A5-4 潤滑油の温度が上がると粘度は下がるので、軸受の性能が低下する。たとえば、負荷容量は小さくなり、ジャーナルの軸心が下がり、小さな負荷となってもそれほどジャーナルは浮き上がらず、より小さな負荷までオイルホイップは起こらないと予想した。運転して確認した結果、その通りとなった。 Q5-5 原因を判定するキーポイントをどのように適用したか? A5-5 回転数は一定で、その他のパラメータ(個々では負荷)が変わることで振動が増大したことから、強制振動の共振ではないと判断すれば、あとは自励振動となる。さらに、真円形状のすべりジャーナル軸受を使っていること、振動の増減にヒステリシス(イナーシャ効果)があることで、オイルホイップいうことになる。 Q5-6 応急対策として、軸受幅を小さくしたのは何故か? A5-6 潤滑油の温度を上げて、粘度を下げたように、軸受幅を小さくして軸受の負荷容量を下げた。その結果、ジャーナルの軸心が下がり、より小さな負荷までオイルホイップが起こらなくなった。また、これはすぐに出来る対策でもあった。 Q5-7 波形観測のため、振動はどこの部分を測ったのか。 A5-7 簡易振動計で、タービンの軸受台の振動を図り、オシロスコープで記録した。 Q5-8 ジャーナルの偏心が小さくなるのはなぜか? A5-8 負荷が大きい時は、上記が全周から注入されるので、ジャーナルは周囲から等しく圧力を受け、ロータ自重と減速装置の歯車の反力が軸受の負荷容量とつりあっている。低負荷になると、下からのみの蒸気で、このつりあいがくずれ、ジャーナルが浮き上がった。 Q5-9 オイルホイップが起こるのは、危険速度の2倍の回転速度だけか? A5-9 典型的な起こり方が危険速度の2倍前後である。しかし、かならずしもそうとは限らない。後述のオイルホイップの特徴や発生メカニズムの項を見ること。 Q5-10 イナーシア効果と負荷の関係は? A5-10 イナーシア効果は負荷がパラメータのときでも同様。負荷の増減にしたがって、発生、消滅の負荷が異なる。事例のデータを見ること。 Q5-11 回転数の半分の成分が何故あるのか? A5-11 回転するものと固定側との平均が半分回転という、あくまで便宜的なもので、ここでの発生メカニズムの簡単な説明がすべてではない。オイルホワールの振動数も回転速度の半分ということではない。 Q5-12 オイルホイップ発生後、回転数をさらに上げるとどうなるか? A5-12 発生がおさまることはない。振動数も変わらない。自励振動で発散する性質を持っているので、非常に危険である。 Q5-13 オイルホイップとオイルホワールの違いは? A5-13 ロータ・軸受系で自励振動が発生する、つまり、系が不安定になりうる場合、自励振動の発生開始速度が危険速度の2倍から離れていれば、まず、オイルホワールが発生する。これはオイルホイップの前兆であり、まだ大きな振動にはならない。危険速度の2倍に近づくとオイルホイップ,おおきな振動となる。このようなことを正確にいうには解析が必要である。 Q5-14 強制振動の対策はどうするか? A5-14 危険速度を定格運転速度から、±30%位離す、十分なつりあわせを行い、最適な軸受を選定し、危険速度通過時の振動を抑える、などである。 Q5-15 プリロード係数とは? A5-15 非真円軸受の非真円度を表す量で、軸受の最小半径すきまを Q5-16 2円弧ジャーナル軸受とは? A5-16 オイルホイップの防止対策(軸受の選定指針)の図を見ること。オイルホイップを考慮した機械でよく使われる。真円軸受より、オイルホイップ防止特性がよいと言える。非真円軸受の内では、比較的安価に作れる。 Q5-17 アライメントとは? A5-17 ここでの事例の対象機械のようなマルチスパンロータを設置する時、軸の静たわみ、熱膨張、軸受荷重の配分を考慮しながら、相互の回転中心線が一致するように機器を配列する。その際、軸受の水平位置、高さを調整する。高さの調整には、軸受台と基盤の間にシム(薄い板)などを挿入する。 Q5-18 シムアップとは? A5-18 最初のアライメント時に、軸受の高さが十分でなかったということで、軸受台と基盤の間にシム(薄い板)を挿入し、軸受の位置を高くした。これによって、軸受荷重が増え、ジャーナルの偏心が大きくなった。 Q5-19 なぜ、No.2の軸受温度が今までより高くなったのか? A5-19 軸受荷重が増え、ジャーナルの偏心が大きくなったことで、軸受すきまが小さくなり、摩擦熱が増加した。ここでは、このことでシムアップがきちんとなされたと判断している。 Q6-1 時間遅れとは、何の何に対する遅れのことか? A6-1 たとえば、一対のロールからなる接触回転系を考えると、接触部は1つである。一対のロール間の力はこの接触部を介してのみ伝達される。この接触部に接触力が加わるとする。次に同じロールの位置に接触力が加わるのはロールが1回転後となる。このロール1回転までの時間帯においては同じロールの位置は外部から何ら影響を受けず、接触部で生じた変形が回復する。このロール1回転の間の時間が時間遅れとなる。 Q6-2 接触回転系2はロールではなく、他の接触系が動く場合にも、パターン形成現象は起こるか? A6-2 パターン形成現象は接触部を有する系であればどんな系でも生じる可能性がある。他の接触系としてうすいフイルム、うすい板(ストリップ)などが動く場合でもロールや他の接触系(フイルム、ストリップ)にパターンが形成される。 Q6-3 最初の変形理由は何か? A6-3 色々あるが、たとえば、接触部に何かが介在すると、それが原因で自由振動を誘起する。産業界で一番多い可能性はロールの表面あらさがあらいときと考えることができる。 Q6-4 パターンが生じると機械にどのような影響を及ぼすか? A6-4 パターンが生じると、通常の機械の運転が不可能になるような大きな振動や大きな騒音が生じる。この振動のために、機械の運転を中止して、部品を交換せねばならないことがしばしば生じる。また、接触回転系でパターン形成が生じると、そのパターンが他の接触体に転写される。たとえば、製鉄機械のロールでは、ロールの表面にパターンを生じるとそれが板などに写ってしまい、板が欠陥製品となることもある。 Q6-5 接触力の変動が起きる理由は? A6-5 パターンが生じるためには振動現象の発生が必要である。パターン形成を生じるためには、振動によって接触部に接触力の変動が生じること、その接触力が大きく変動すること、接触力の変動によって変形が発生・成長することが必要である。したがって、一般に、高次の振動モードほどパターン形成は生じやすいことになる。 Q6-6 上下ロールの変化に違いはあるか? A6-6 抄紙機の一対のゴム巻きロールは、一般に硬いゴムを巻いたロールとそれよりもやや柔らかいゴムを巻いたものからなっている。そのため、柔らかい方のロールのゴムにパターンが形成されやすい傾向がある。しかし、硬い方のゴムも程度は低いものの変形を生じていると思われる。上下ロールの直径が異なるともっと複雑な変形形態を生じる。 Q6-7 タイヤの多角形摩耗を防ぐにはどのような対策があるか? A6-7 自動車タイヤの多角形摩耗を防止するためには、高速道路などで一定の走行速度で長時間走行しないこと、トーインを大きくとらないこと、タイヤ空気圧を高めにすることなどが現在の個人でできる対応策である。 Q6-8 ドライブロールの回転速度を変化させると振動はどう変化するか? A6-8 ドライブロールは一定回転数で回転するが、ボビンホルダは弾性糸が巻かれるにつれて回転数は遅くなる。ドライブロールの回転数を高くすると、糸玉のパターンの角形数は小さくなる。一方、ドライブロールの回転数が低くなると、糸玉のパターンの角形数は大きくなり、生じにくくなる。 Q6-9 下ワークロールは変形しないのか? A6-9 下ワークロールにもわずかにパターンが生じることがあるが、上ロールに比較すると問題にならない程度である。しかし、下ワークロールにもパターンを生じる別の振動がある。それはロールとプレートの間の摩擦が大きく、振動数が高いときに起こる。通常の産業界の機械では上ロールのみのパターン形成現象がほとんどであるが、これは、上ロール系の固有振動数が下ロール系よりも固有振動数が低いのが1つの原因である。 Q6-10 多角形穴にしないためにはどうすればいいか? A6-10 ドリルをゆっくり回転させることが必要である。それ以外に、ドリルの先端(チゼルエッジ)にさらに小さなドリルを取り付ける方法も効果的である。 Q7-1 磁気軸受の磁気吸引力の求め方は? A7-1
磁気軸受はどのような機器に使われているか? A7-2
磁気軸受の規格はどうなっているか? A7-3 磁気軸受の実用化を促進するために日本機械学会に磁気軸受標準化研究会を結成し、さらに工業技術院からの再委託として ISO/TC107/SC2/WG7
磁気軸受国内委員会が中心となり、磁気軸受に関する「ISO規格」、「ISO技術指針」、「機械設計者のための磁気軸受設計マニュアル」を作成しつつある。
磁気軸受の制御について知りたい。 A7-4
磁気軸受の磁極の形状はどのようになっているか? A7-5
磁気軸受の特徴を知りたい。 A7-6 大型の回転機械に使われる磁気軸受はほとんど8極型磁気軸受である。
設計過程ではどういったチェックが行われるか? A8-1 設計時に設定した風速に対してフラッタが発生しないかどうかチェックする。 この場合、平板又は翼のまげとねじりの運動方程式を立てる(ねじりの場合回転中心を求める)。 次に、揚力とモーメントの式と揚力中心を求め、それらの値を運動方程式に代入してフラッター速度を計算し、求めた速度が設定風速より低い場合はフラッタ対策で記述したような対策をとり、フラッタ流速を上げる。 Q8-2 フラッタ以外の自励振動の例としては、どういったものがあるか? A8-2 フラッタ以外の自励振動はたくさん存在する。エネルギ源として、風以外に一定の力、一定の電磁力一定の回転力(回転機械)などがある。代表的な例をいかに示す。
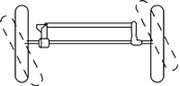
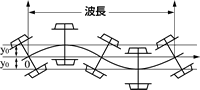
行きと返りの仕事が違うとはどういうことか? A8-3 変位と力の関係を表すグラフにおいて、仕事は”力 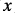 変位”であるから、変位xが増大する方向へ物体がA点からB点に移動する場合の力の大きさ 変位”であるから、変位xが増大する方向へ物体がA点からB点に移動する場合の力の大きさ同様に帰りの仕事 したがって1サイクル振動する時の仕事 この仕事が正負の場合により、以下のようになる。
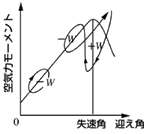
他のフラッターとして失速フラッターはどのようなメカニズムでしょうか? A8-4 失速角付近での気流のはく離によってひきおこされる、ねじり振動を主とする翼のフラッタである。ねじり振動を行う翼では、同じ迎え角でも、迎え角が増す場合と減る場合では、気流の状態が異なり、1回の振動中に翼に働く空気力のモーメントは図のようになる。空気力のなす仕事Wは、失速角以下では負であるのに対し、失速角付近では正となる。このため負減衰モーメントが働き、振り幅が増大する。 Q8-5 微小外乱にはどういったものがあるか? A8-5 微小外乱とは自然界に存在する人体には感じられない程小さな外乱でもよいので、いろいろなものがある。フラッタの発生に影響の大きなものとして、微小な振動、風の変動、気温や熱の変化などがある。 Q8-6
Q8-7 Q8-8 揚力の発生が少なくなるような流体力学的配慮の例として、どのような方法が挙げられるか? A8-9 揚力の発生を少なくするような構造は吊り橋などで用いられるが、その例として次のようなものが揚げられる 1)断面形状で前縁および後縁に気流を乱すようなものを取り付ける 2)断面の中央にスリットを入れて、上下面の圧力差が大きくならないようにする Q9-1 摩擦振動とは? A9-1 摩擦振動とは、摩擦の特性に起因する自励振動で、大きく2種類の現象がある。 その発生メカニズムはこれからの画面で説明する。 Q9-2 指数関数的に成長する振動とは? A9-2 式で表現すると、振動の変位を Q9-3 なぜ負荷の部分を打撃したか? A9-3 問題となる振動のモード成分が大きいところを打撃すると、その振動がでやすい。 Q9-4 自励振動と強制振動の特徴は? A9-4
Q9-5 摩擦は振動の減衰に効くのではないのか? A9-5 確かに、摩擦を利用したダンパーなど減衰に効果のある場合もある。摩擦により振動エネルギを消散すれば、減衰になる。特に静止状態を中心に、速度の方向が変化するような場合には、減衰として効果がある場合が多い。ただし、後述の場合にように、摺動部摩擦により振動エネルギが流入する場合もある。その場合には、静止状態が中心ではなく摺動面が動いている状態を中心とした振動となる。 Q9-6 なぜ摩擦による自励振動と判断したのか? A9-6
Q9-7 摺動部の潤滑は、どのようになっているか? A9-7 摺動部は最初はグリースによる潤滑がなされていた。2硫化モリブデンのスプレーを吹き付けると潤滑状態が改善した。 Q9-8 スティックスリップの例としては、どのようなものがあるか? A9-8 油圧系では、油圧シリンダとロッドの間では油がもれないようにする必要がある。ロッドが動く時に、ロッドとシリンダとの間の摩擦によってスティックスリップが発生する場合がある。 バイオリンで音がでるのはスティックスリップによるものである。弓と弦の間の摩擦によって弦が振動して音がでる。現象としては、1自由度の場合よりも少し複雑になる。 Q9-9 事例の現象がスティックスリップではないと判定したのはなぜか? A9-9 以下のような判定理由がある。
Q9-10 剛性マトリックスに非対称な項が、自励振動の原因になるのはなぜか? A9-10 これは、回転機械における有名な自励振動であるオイルホイップなどと同様の現象である。詳細はレッスン5参照。 Q9-11 なぜ下降では自励振動が発生し、上昇では発生しないのか? A9-11 上昇の場合には、2つの非対称項の符号は必ず等しいが、下降の場合には、条件を満たせば、2つの非対称項の符号が異なる。符号が等しければ、運動方程式を変形して対称な形に変形できるので、不安定になることはない。詳細は以下の文献参照。 桜井明、井上喜雄、筒井秀実、伊藤廣、しゅう動部摩擦を介した非対称連成力による自励振動に関する研究、日本機会学会論文集C編、60巻570号 (1994)p.380-385 Q10-1 誘導電動機の騒音が最近とくに問題になるのはなぜか? A10-1 なぜ電磁騒音が問題になるかというと、騒音レベルもあるが、特定の周波数のところで大きな騒音が発生するため、これが人に不快な音として聞こえてくる。工作機械のような騒音は、特定の周波数というわけではなく周波数全体に騒音が発生している。このため、全体としての騒音を低減すればそれほど気にならない。  Q10-2 電動機の騒音はどのような原因から発生しているのか? A10-2 ここに、モータの振動・騒音を分類してみた。この場合は、誘導電動機ばかりでなく、直流モータ、永久磁石モータなども対称になっている。このように多くの騒音があり、発生周波数、騒音源が異なるので注意が必要である。また対策も当然異なってくる。 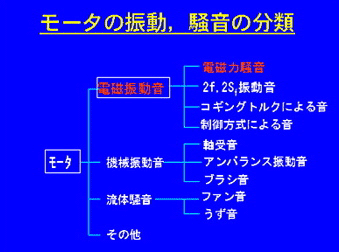 Q10-3 電磁力が加振するメカニズムは? A10-3 交番磁界によって回転子と固定子にある周波数を持つ周期性のある力が作用し、固定子からフレームに伝わってフレームを振動を発生させ騒音となる。 Q10-4 高調波成分とは? A10-4 電気的な特性によって基本周波数がきまり、この整数倍の周波数を持つ成分のこと。たとえば2極の電動機の場合には関東地方では50Hz、関西地域では60Hzが基本周波数となる。 Q10-5 高調波成分が騒音の源となる原因は? A10-5 基本周波数は一般に低く人間の耳にそれ程不快感を与えないが、高次成分になると周波数も高くなり、人間の耳に敏感に反応するため、大きかったり、いつまでも残るような音として不快感を感じる。 Q10-6 有限要素法や境界要素法とは何か? A10-6 連続体を解析するときに用いられる解析手法。その使い方は解析目的によって異なるため、十分に注意が必要である。 Q10-7 実際の騒音はどの程度か? A10-7 環境や時間帯によってそのレベルは異なるが、参考までに示すと、日常的に事務室で静かに感じるときは30から40dB、騒々しいと感じるときは40〜50dB、街頭では乗用車が通過すると60〜70dB、小型トラックで70〜80dB、大型トラックで80〜90dBである。電車や地下鉄の車内は65〜75dBである。(出典:機械騒音ハンドブック、日本機械学会編、産業図書、1991) Q10-8 設計段階でシミュレーションはどの程度行われているのか? A10-8 振動や騒音についてはまだまだシミュレーションの利用は少ないが少しずつ増えてきている。今後、設計のIT化が進むにつれて、開発期間短縮、コスト低減に向けてその割合は大幅に増加してくるものと予想される。ただし、この場合構造のモデル化が重要になる。 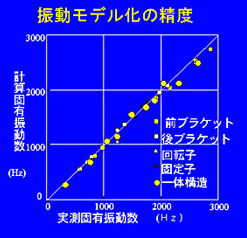 振動モデルを構築する場合には、その精度について十分検証しておく必要があるが、この場合は、モータを前ブラケット、後ブラケット、回転子、固定子(コイル-ハウジング)に分けた。それぞれに対して、打撃試験と計算から固有振動数とモードを求め、計算値が実測値に一致するまで、ヤング率や密度等を変化させる。このようにして求めたヤング率や密度等を用いてモータを組み合わせたときの固有振動数やモードを計算で求める。この組み立てたモータの計算値と実測値との差を求め、誤差が大きい場合は再度部品ごとの計算に戻る。このようにして、最終的にモデルの高精度化を確認する。 Q10-9 理想的な設計でのこれら2つの関係はどのようなものか? A10-9 試作をしなくても低振動、低騒音モータの開発が可能になることが理想である。 Q10-10 円環次数とは? A10-10 円環モードに下から順に番号付けしたものを円環次数と呼ぶ。 Q10-11 リブとは? A10-11 身体でいえば骨のようなもので、やわらかいところを補強してかたくする役割を持つもの。 Q10-12 リブをつけることで得られる効果は? A10-12 電磁力と構造の共振を避けることが可能となり、騒音が低減される。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 を取り囲む閉曲線Cに沿った磁界H
(Magnet Field Intensity) の周回積分は
を取り囲む閉曲線Cに沿った磁界H
(Magnet Field Intensity) の周回積分は (1)
(1) の場合には
の場合には (2)
(2) (3)
(3) (Flux density)とおくと、
(Flux density)とおくと、  の関係がある。 ここで
の関係がある。 ここで  は真空中の透磁率で
は真空中の透磁率で
 (7)
(7) を磁気抵抗と呼ぶ。式(7)は起磁力を電位差、磁気抵抗を電気抵抗、磁束を電流と読みかえると、電気のオームの法則に対応している。磁気回路についてもキルヒホッフの法則が成立する。
を磁気抵抗と呼ぶ。式(7)は起磁力を電位差、磁気抵抗を電気抵抗、磁束を電流と読みかえると、電気のオームの法則に対応している。磁気回路についてもキルヒホッフの法則が成立する。 であるので、
であるので、 (9)
(9) は継鉄の飽和磁束密度
は継鉄の飽和磁束密度
 から
から (10)
(10) であり、磁極に強磁性体を使用する場合
であり、磁極に強磁性体を使用する場合









 国際標準化機構(ISO)のTC108(機械振動と衝撃、設備の監視と診断/SC2(機械振動)/WG7(磁気軸受)を日本からの提案で結成し、これを日本機械学会磁気軸受標準化研究会と
ISO/TC107/SC2/WG7 磁気軸受国内委員会が支援し、次の項目を実施している。
国際標準化機構(ISO)のTC108(機械振動と衝撃、設備の監視と診断/SC2(機械振動)/WG7(磁気軸受)を日本からの提案で結成し、これを日本機械学会磁気軸受標準化研究会と
ISO/TC107/SC2/WG7 磁気軸受国内委員会が支援し、次の項目を実施している。 はゲイン余裕、
はゲイン余裕、 は位相余裕と呼ばれている。WG7ではこの
は位相余裕と呼ばれている。WG7ではこの  を“Distance Margin”と規定している。またあるメーカーはこの数値の逆数である感度関数の最大値で磁気軸受システムの安定性を評価している。
ナイキスト安定判別法で用いる位相余裕とゲイン余裕は Distance Margin の近似値である(図3参照)。
を“Distance Margin”と規定している。またあるメーカーはこの数値の逆数である感度関数の最大値で磁気軸受システムの安定性を評価している。
ナイキスト安定判別法で用いる位相余裕とゲイン余裕は Distance Margin の近似値である(図3参照)。

 (1)
(1) (2)
(2)


 は磁気軸受の制御剛性、不平衡剛性と呼ばれる。
は磁気軸受の制御剛性、不平衡剛性と呼ばれる。 (5)
(5) は
は  のラプラス変換である。
のラプラス変換である。 (7)
(7) を選定すれば、安定で定常偏差を生じることも無い。
を選定すれば、安定で定常偏差を生じることも無い。

 (1)
(1) (2)
(2) (3)
(3) 、
、 、
、 (4)
(4) (5)
(5) となり式(5)より、
となり式(5)より、
 である。
である。 、式(1)から、
、式(1)から、
 から次式が導出される。
から次式が導出される。 (6)
(6) 軸受と軸が同心のときの軸受と軸の間の隙間である。
軸受と軸が同心のときの軸受と軸の間の隙間である。
 (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11a)
(11a) (11b)
(11b) (11c)
(11c) (11d)
(11d) が導かれる。この磁束とy方向の加重が次のように導かれる。
が導かれる。この磁束とy方向の加重が次のように導かれる。 (13)
(13) (14)
(14)
 (15)
(15) (16)
(16) (17)
(17) であるので、
であるので、
 のみによって磁気力が発生する。
のみによって磁気力が発生する。 (18)
(18)
 (19)
(19) (20)
(20) (21)
(21)

 が正の場合
が正の場合