|
Q1-1.「きつつきのおもちゃ」と同じ現象を利用したものにはどんなものがあるか? Q1-2.「危険速度」を考えずに作られた列車では、全ての列車で異常振動が発生したのか? Q1-3.振動には他にどのようなものがあるか? Q1-4.ダッシュポットは、実際にはどのようなものか? Q2-1.自由体図を書くときには、どのような注意が必要か? Q2-2.慣性モーメントとはどのようなものか? Q2-3.ラグランジュの運動方程式を使うことによる利点は何か? Q3-1.sinθをθと置けるのはなぜか? Q3-2.ばねマス系では固有振動数は何に依存するか? Q3-3.変位振幅率とは何か? Q3-4.力加振と変位加振の違いは? Q3-5.「ζ」の物理的意味は何か? Q4-1.K1=K2のとき、剛性行列以外の成分に特徴はないのか? Q4-2.解を正弦波と仮定するのはなぜか? Q4-3.2つの質点が強制振動数をあげていくと、同相になったり、逆相となったりするのはどの式で確認できるのか? Q4-4.動吸振器を使用している身近な機械は何か? Q4-5.ダンパの仕組みはどうなっているのか?また、その種類はたくさんあるのか? Q5-1.モード試験の意義は何か? Q5-2.周波数応答関数とは何か? Q5-3.実際の建築・土木構造物は大きいが、どのように実験モード解析を行うのか? Q5-4.精度良い周波数応答関数を得るためには何回程度の計測を行って平均化処理するのが理想か? Q5-5.FFT装置が無い時代にはどうしていたのか? Q5-6.測定点は、どの程度の数を取ればよいか? Q5-7.なぜ加振点で計測を行わなければならないのか? Q5-8.ボード線図とは何か? Q5-9.画面7に現れる近似式の右辺第2項の物理的意味はなにか? Q5-10.最尤推定法とは何か? Q5-11.ローパスフィルターとはなにか? Q6-1. ゴム,空気ばねはどのような所で用いられているか? Q6-2.振動問題とは具体的にどのようなものがあるのか? Q6-3.他にアクティブ制振装置はどのような場面で用いられるか? Q7-1.振動が非線形であるか線形であるかの違いで、ゆれの感じ方に違いは生まれるのか? Q7-2.シートにガタがない場合は、どのような振動になるのか? Q7-3.ウレタンフォームの伝達関数の設定時に、不快振動の循環はどのように考慮されているのか? Q7-4.この変位-荷重特性からはばね定数をどのように求めるのか? Q7-5.ヒステリシス損と減衰力は同じものなのか? Q7-6.ランダム振動入力とは、具体的にはどのようなことをすることなのか? Q7-7.単一の調和励振とはどのようなものなのか? Q7-8.相対変位とは、何と何の相対変位なのか? Q7-9.線形ばねにおいて、具体的にどういった場面で重ね合わせの原理が使われるのか? Q7-10.硬化ばね、軟化ばねにはどんなものがあるのか? Q7-11.磁石ばねはどのようなところで使われているのか? Q7-12.(b)、(c)、(d)の共振は、どのような場合に発生するのか? Q7-13.この磁石ばねに限らず、ばね力がf(x)=k1x+k2x2で表されるばねには1/2次分数調波共振が発生するのか? Q8-1.風による送電線の振動では、負性抵抗がどのように働いているか? Q8-2.チョークの振動ではどのようにモード連成が起こっているのか? Q8-3.自由振動と強制振動の違いは何か? 08-4.並進ギャロッピングを防ぐ方法はあるのか? Q8-5.渦励振を防ぐための工夫にはどのようなものがあるのか? 08-6.スロッシングとはどのようなものか? Q9-1.往復動機関と速度形機関はどう違うのか? Q9-2.往復運動と回転運動間の変換機構には、この他にどんなものがあるのか? Q9-3.連接棒の最大慣性モーメントと、それを生じるθの値を出すことはどのような意味をもつのか? Q9-4.ここで、ピストンに加わる慣性力は考慮したのに、連接棒に加わる慣性力は考慮しなかったのはなぜか? Q9-5.大きな慣性モーメントを持つはずみ車とはどのようなものか? Q9-6.エネルギーの吸収または放出はどうして起こるのか? Q9-7.角速度変化量と慣性モーメントの関係式はどのようにして出てきたのか? Q9-8.なぜはずみ車の慣性モーメントはΔE1から得られるのか?ΔE2やΔE3ではだめなのか? Q9-9.mc、mrp、mrcがこのように表せる理由は何か? Q9-10.慣性力を1次慣性力、2次慣性力と分けることは、どのような意味があるのか? Q9-11.多気筒の場合、回転部質量を0にすることは可能か? Q9-12.回転部質量に対するつりあい錘と往復部質量に対するつりあい錘は同じものなのか? Q9-13.実際は、過分つりあわせと部分つりあわせのどちらがより使われているのか? Q9-14.なぜ多気筒小容量機関を使えば大馬力を作ることができるのか? Q10-1.軸受から受ける力、回転体に作用する不安定化力、熱応力の中で特に注意するものは何か? Q10-2.減衰器を除いたモデルで考えても、実際の動きとの違いは生じないか? Q10-3.材料力学の公式とはどのようなものか? Q10-4.コマのこのような性質はなぜ生まれるのか? Q11-1.ひとつひとつの部品を分けて考えることは当たり前のような気がするが、部品をまとめて扱うこともあるのか? Q11-2.マルチボディシステムとは何か? Q11-3.一般化座標が独立とはどういうことか? Q11-4.時間tが拘束条件に含まれるものにはどんなものがあるか? Q11-5.拘束条件を微分したものが拘束条件式を一般化座標で偏微分したものと一般化座標の微分の積となるのはなぜか? Q11-6.m>nとなることはないのか? Q11-7.ここではθを独立一般化座標としたがxやyを独立一般化座標としてもよいか? Q12-1.曲げモ−メントの効果とはどのようなものか? Q12-2.調和振動とは何か? Q12-3.Cは任意の値でよいのか? Q12-4.AiとBiも無限個存在するのか? Q12-5.有意なモードはどのくらいあるのか? Q1-1 「きつつきのおもちゃ」と同じ現象を利用したものにはどんなものがあるのか? A1-1 「きつつきおもちゃ」は「摩擦振動」が作用して、あの動きになっている。摩擦振動についてはレッスン8「自励振動」の中で5番目に「摩擦振動」の授業があるので、そこで参照のこと。おもちゃの動きに対して、動作原理が説明できないものもある。 身の回りおもちゃを見直すと、発見がある。同じ摩擦振動を利用したおもちゃをここに示す。図1は同じ動作で、付けてある模型が違うもの。図2は糸の振動と摩擦を利用した物で「まさる」と言う。土鈴がついていて音を出しながら下降する。また、図3は「歩く馬と宇宙人」と呼ばれているもので、よたよた坂を下りていくか、重りに引かれている。 おもちゃを科学する参考書としては「おもちゃの科学」(全6巻、戸田盛和著 日本評論社)がある。また他に、絶版になった参考書も何冊かある。
Q1-2
振動には他にどのようなものがあるか? A1-3 画面では、ばね・質量系の振動を例にとった。振動関係の問題は多くあるが、その一部としてレッスンの「6.固有振動数について」に固有振動数の例がある。それを見ると分かるとおり、固体、液体の各種振動が掲載されている。それ以外では、笛が筒中の気体の振動により音を出すように、気体も振動する。このように、身の回りの事象を見直してみると、色々な発見がある。 Q1-4 ダッシュポットは、実際にはどのようなものか? A1-4 実物の例を下記に示す。また、一般的な粘性減衰係数の表も掲載する。既製品では、目的に応じて、直線、揺動、回転運動用と用意されている。
Q2-1 自由体図を書くときには、どのような注意が必要か? A2-1 自由体図を書くときには、図の中に隠れている情報を見落とすことなく列挙することが大切である。隠れている情報には、重力、モーメント、反力といったものが挙げられる。 Q2-2 慣性モーメントとはどのようなものか? A2-2 軸まわりの回転のしやすさを表す指標で、直線運動の場合の質量に対応するもの。 Q2-3 ラグランジュの運動方程式を使うことによる利点は何か? A2-3 2自由度以上の自由度を含む系の運動に関する運動方程式を求める時、力とモーメントの釣り合い式を幾何学的関係から求めようとすると、考えにくかったり、ミスを犯したりするが、ラグランジュの運動方程式を用いると、エネルギーを間違えることなく記述できた後は、機械的操作で運動方程式を導出できるという利点がある。 Q3-1 sinθをθと置けるのはなぜか? A3-1 正弦関数を書いてみればわかるとおり、θが微小な範囲では、sinθとθはほぼ一致する。しかし、これは近似であるため、振子システムの厳密な運動方程式を求めるときには、このような近似はおこなわず非線形な方程式で記述することになる。 Q3-2 ばねマス系では固有振動数は何に依存するか? A3-2 運動方程式に現れる振動を表す物理量は、質量とばね定数である。よって、この2つの物理量に依存する。質量と加速度により慣性力が求まり、ばねによる力とつりあうことで振動系が定まる。 Q3-3 変位振幅率とは何か? A3-3 強制振動の特徴は、加振振動数によって、振動振幅が異なることである。この特徴を記述するのに、変位(すなわち振幅)の絶対値ではなく、無次元量で記述するほうが合理的である。そのため、基準となる振幅として、静的な状態での変形量を用いて無次元化し、その倍率で示すことになる。一般的にゲインともよばれ、このような無次元化は工学分野での一般的な手法である。 Q3-4 力加振と変位加振の違いは? A3-4 振動系に直接周期的な外力が作用するのが力加振であり、直接力は作用しなくても、振動系を構成するばね要素を、強制的に、かつ周期的に動かすことによる加振が変位加振である。前者は運動方程式上分かりやすいが、実際の場面においては、地震による加振、車両の走行による振動など、変位により加振される状況がかなりある。 Q3-5 「ζ」の物理的意味は何か? A3-5 速度に比例する抵抗力である粘性減衰を特徴づける物理量として、運動方程式に現れる速度に比例する比例係数である減衰係数があるが、これの無次元化したものと考えられる。減衰振動の物理的特徴として、もっとも振幅が早くおさまる臨界減衰状態があるが、そのときの減衰係数を用いて無次元化したことになる。 Q4-1 K1=K2のとき、剛性行列以外の成分に特徴はないのか? A4-1 バネは変位に応じた力を生成する.このことからバネ定数は剛性行列の成分中にのみ現れ,剛性行列以外の成分には関係しない. Q4-2 解を正弦波と仮定するのはなぜか? A4-2 ここで扱った系が線形システムであると仮定するためである.線形システムとは,ある振幅と周波数の正弦波入力に対して,質点の位置,速度といった出力が同一周波数の正弦波となる系である.また入力と出力の周波数は同じだが,出力振幅は入力振幅を周波数に応じて拡大したものとなる.本講義における2自由度振動系では,振動振幅を変数とした正弦波を解として代入することで実際に解が求まっているので,この系が線形システムであるという仮定は正しかったことになる. Q4-3 9-1・2つの質点が強制振動数をあげていくと、同相になったり、逆相となったりするのはどの式で確認できるのか? A4-3 共振曲線は振幅の絶対値で表示していたが,絶対値を用いない振動振幅の式の正負によって確認できる.振動振幅が正のとき同相,負のとき逆相となる. Q4-4 4-1・動吸振器を使用している身近な機械は何か? A4-4 鉄道車両は旅客が乗る車体の下に台車枠があり,その下に車輪が取り付けてある.台車枠が動吸振器の作用をもつことで,車輪がレールのゆがみによって生じる上下振動をなるべく車体に伝えないよう最適化した構造を実現している.他にも高層建築物の上層階に動吸振器を取り付け,地震や風による建物の振動を逓減するといった応用例もある. Q4-5 ダンパの仕組みはどうなっているのか?また、その種類はたくさんあるのか? A4-5 (油圧ダンパの仕組みについては「1自由度振動系」に説明がある).ダンパは用途に応じて非常に多くの種類のものが存在する.速度に比例した減衰力を発生する粘性ダンパとして非常に広範に使用されるものは油圧ダンパといわれるものある.これは油が弁を通過するときに生じる流体抵抗によって減衰力が発生する.また,磁気ダンパは構造物の振動エネルギーを永久磁石と導体との間に生じる渦電流に変換し,熱エネルギーにして消散させることで比例減衰を得ることができる. Q5-1 モード試験の意義は何か? A5-1 最も基本的意義は、対象構造物の固有振動数(または共振振動数)を計測できる点である。次の意義は、それらの固有振動数に対応する固有モード(その共振振動数の正弦波で構造物を定常振動させた場合の構造物の振動する形と解釈してよい)を実験的に明らかにすることができる点である。さらに、それぞれの固有モードにおける減衰特性(通常モード減衰比で表現する)も定量的に求めることができる点である。モード試験から得られるそれらのパラメータをモード特性と呼ぶ。 より高度な応用面からの意義としては、そのモード特性を利用して、任意に構想される構造変更をその構造物に施した場合には共振周波数などがどのように変化するかを予測解析することができるという点が挙げられる。 Q5-2 周波数応答関数とは何か? A5-2 本学習の第1画面中で概略解説しているが、次のように解説してみよう。対象構造物のある1点を、ある周波数ωの正弦波の力で定常加振している状態を考える。その加振状態下の構造物上の任意の点の振動応答を計測すると、やはり同じ周波数の正弦波になる。 その振動応答を表現する正弦波の振幅の値を、加振力を表現する正弦波の振幅の値で割り算した値が、周波数ωでの周波数応答関数の振幅(ゲイン)である。また、加振力の正弦波を基準に観測される振動応答の正弦波の動きのずれを周波数応答関数の位相と呼ぶ。 これらの振幅と位相は周波数ωに依存して異なった値となる。多くの周波数についてそれらをプロットしたものの1例が、本学習の第4画面などにボード線図として示されている。周波数応答関数は入力信号とそれに起因して観測される応答信号の関係を周波数成分毎に表現した関数で、伝達関数と呼ぶこともある。 Q5-3 実際の建築・土木構造物は大きいが、どのように実験モード解析を行うのか? A5-3 建築・土木構造物は一般に大きいので、大きな加振力で加振してモード試験を実施する必要がある。そこで、本学習画面で紹介表示した打撃試験用ハンマーと同類で杭を打つためのような大きなハンマー(重量約15kg、最大加振力約2000kg)などが市販されている。また、不つりあい円盤を回転させて回転不つりあい力により加振力を発生させる大型の加振機も開発されている。サーボをかけてリニアガイド上で大きな質量ブロックを正弦波状に振動変位させて、その反力で加振を行う加振機もある(写真はその一例である)。これらを橋梁上や建物内部に設置して振動試験を実施する。 これ以外にも一風変った加振方法もあるが、ここでは紹介を省略する。振動応答の計測については、建築・土木構造物は大きいために対象とする振動周波数帯域が低いので、それに十分対応した高感度の加速度計が一般的に使われる。それにしても構造物が大きいので、センサー配置や信号ケーブルの配線なども大掛かりになり、多大な費用がかかる。
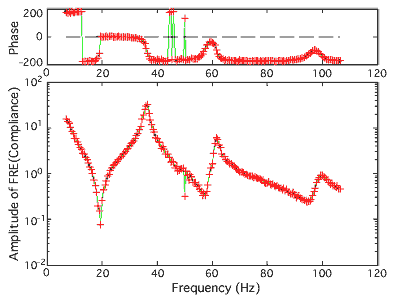
Q5-4 精度良い周波数応答関数を得るためには何回程度の計測を行って平均化処理するのが理想か? A5-4 一概に何回とはいえない。打撃試験では、現実的な手間とマニュアル操作の繰り返し精度の観点から、4回程度の平均化が必要であろう。 加振器を利用する場合には、まず平均回数を多く設定して試しの計測を行う。計測装置の画面上で一回一回平均化処理していく過程で周波数応答関数とコヒーレンス関数がどのように変化していくかを観察する。この観察により何回程度平均化すると周波数応答関数とコヒーレンス関数が収束するかがわかる。その回数を平均化回数として設定して、試験を開始すればよい。 加振波形の種類や構造物の特徴に依存するが、通常は4回から32回程度の範囲となると思われる。また、ランダム波加振の場合は比較的多くの回数を設定することになるであろう。 Q5-5 FFT装置が無い時代にはどうしていたのか? A5-5 FFTアルゴリズム提案の論文は1965年である。それまでは、正弦波加振により加振力の正弦波信号と振動応答の正弦波信号をアナログ電圧信号としてXYプロッタに入力して記録用紙に記録し、その記録紙に物差しを当てて読み取ることで、共振振動数や共振振動モードを描いていたため、非常に時間を要し、苦労の多い試験だったそうである。 記録用紙に物差しを当てて読み取ることを改善するために、トラッキングフィルターと呼ぶ非常に急峻で周波数を自動的に一定速度で変化させることができる2チャンネルもしくは多チャンネルのバンドパスフィルターとアナログ演算回路から構成される装置も開発市販され、利用されていた。振動応答信号を加振力信号でアナログ的に割り算し、結果(周波数応答関数)をアナログ電圧信号として出力し、それをXYプロッタなどで記録した。 デジタルコンピュータとFFTアルゴリズムの開発により、打撃ハンマーによる衝撃力やシグナル発生器による広帯域波(たとえばランダム波)の信号を利用することができるようになり、モード試験(振動試験)は飛躍的に作業効率とデータ精度が良くなった。 Q5-6 測定点は、どの程度の数を取ればよいか? A5-6 共振振動数(固有振動数)とモード減衰比だけを知りたければ、極端な場合には1点のみの計測でOKである。ただし、この場合もある共振振動については振動しない位置の1点を偶然に計測点としてしまい、その共振振動数を認知できない恐れがあるため、2,3点測定点を変更して計測することになるであろう。 モード試験は、共振振動数だけでなく、固有モード形も求めることが標準である。この場合には、結果論的説明になるが、求めたい最高次数(その固有振動数が計測対象の中で最高)の固有モード形を測定点間を線で結んで描く図として妥当に描ける程度の測定点数を必要とする。 また、応用解析として構造変更解析を想定した試験では、構造変更のための付加質量や補強部材を取り付けようと考えている位置に適切な数の測定点を設定してモード試験を実施する必要がある。そのために測定点数を多少増やす必要が生じる場合がある。 Q5-7 なぜ加振点で計測を行わなければならないのか? A5-7 7番目の画面で説明があるように、定量的に固有モードを測定点の位置の成分で構成されるベクトルデータとして得るために必要である。すなわち、モード解析の理論式中に表れる固有モード成分の個々の値を決定するためには、自己周波数応答関数に関するモード特性同定法を実施して加振自由度に対応した成分を求める必要があるためである。 また、別の便宜的視点からとして、モード試験実施上の測定システムの妥当性をチェックするためにも自己応答周波数関数をまず最初に計測してみることは有意義である。すなわち、ボード線図でその周波数応答関数を描いて観測する場合に、振幅(ゲイン)曲線に関して、各共振峰の間にかならず反共振溝がひとつずつ存在するはずであり、その位置で位相の反転が発生している。位相は、コンプライアンス(変位応答に関する周波数応答関数)の場合にはマイナス180°から0°の範囲、モビリティー(速度応答に関するそれ)の場合にはマイナス90°からプラス90°の範囲、アクセレランス(加速度応答に関するそれ)の場合には0°〜プラス180°の範囲になるはずである。この特性の観察により、センサー、増幅器や計測システム内に組み込まれているフィルタなどの位相特性性能が十分精度良いかどうかをチェックできる。 なお、単に固有モードの形を定性的に(すなわちコンピュータ画面のアニメーション表示などで)観察したいだけであれば、かならずしも自己周波数応答関数を計測する必要はない。 Q5-8 ボード線図とは何か? A5-8 横軸を振動数(または周波数)として、周波数応答関数の振幅を縦軸に表示した図と縦軸に位相を表示した図を上下に組み合わせてできる周波数応答関数を表示するための図の一種である。ここに例を示す。本学習画面では、第4画面の最後に表示された「周波数応答関数の位相」と「周波数応答関数の振幅」の上下2つの図の組合わせがボード線図である。第6画面や第10画面にもボード線図が表示されている。 ボード線図(Bode線図)が最も広く利用されているが、それ以外の線図として、下に例を示すように、コクアド線図(CoQuad線図)やナイキスト線図(Nyquist線図)などもある。コクアド線図は、横軸を振動数(周波数)として、周波数応答関数(各振動数の周波数応答関数は複素数で表現されているので)の実数部の表示図と虚数部の表示図を上下に組み合わせて表示する図である。ナイキスト線図は、横軸が周波数応答関数の実部の値、縦軸がその虚数部の値として、望みの周波数帯域に関する周波数応答関数をプロットする図のことである。
Q5-9 画面7に現れる近似式の右辺第2項の物理的意味は何か? A5-9 右辺第2項は、同定対象周波数帯域内に現れている複数の共振振動数に対応した周波数振動成分を表す式を加算している。すなわち、振動を表現するのに、その固有モードを基底ベクトルとした1次結合で表現(これがモード解析の基本原理)すると、多自由度の振動は、1自由度振動系の単純な重ね合わせで表現できる。 Q5-10 最尤推定法とは何か? A5-10 統計推定学理論の一種で、ごく単純な例を用いて簡潔に解説すれば次のようになる。 本来理論的にはある一定値となるべき物理量ではあるが、無限に多くの回数観測を行い、それらの値xの違いによる度数分布(確率密度分布)をプロットできたとしたら、誤差の混入のために、下図に示すように、度数が最大となる値を中心に左右対称の分布形状を示す物理量があるとする。この形状の分布をガウス分布と呼ぶ。これは誤差のために発生する分布と考える。したがって、観測値に含まれる誤差がガウス分布する性質のものであるともいえる。そこで、理論的なその物理量の値は、度数分布(確率密度または尤度と呼んでよい)の最大となる横軸の値であると考える。これが最尤推定法の基本理論である。 その真の物理量の値をp、ガウス分布の母分散を  とすると、そのガウス分布曲線は数式で、 とすると、そのガウス分布曲線は数式で、 のように表現できる。この成立の仮定下で、実際にその物理量をn回繰り返して観測したところ x1、x2、x3、・・・、xn の値が得られたとする。これらの実際に得られた有限個(n個)の観測(計測)データを利用して、真の物理量の値を推定する。今回x1、x2、x3、・・・、xnの値が得られたのは、それらの値をそれぞれ上の関数に当てはめて計算される値の乗算が最大になったからであると理論立てる。すなわち、確率密度関数(尤度)が最大となっていたからそれらの値が実際に得られたのだと解釈する。数式で示せば、  となる。母分散  には、標本分散を代理で代入して、このLの値を最大にするpの値を求める。その値を、利用した実測データに基づく真の物理量の最も良い推定値であると解釈する。これが最尤推定法である。 には、標本分散を代理で代入して、このLの値を最大にするpの値を求める。その値を、利用した実測データに基づく真の物理量の最も良い推定値であると解釈する。これが最尤推定法である。
Q5-11 ローパスフィルターとは何か? A5-11 ローパスフィルター(Low Pass Filter)は、処理対象の時間信号を入力して、設定した周波数の値よりも高周波の信号成分をふるいにかけて取り除き、低周波成分だけから構成された時間信号を出力してくれる装置である。アナログ電気回路でアナログ的に機能を達成するアナログフィルターとデジタル回路で演算処理するデジタルフィルターがある。 Q6-1 ゴム,空気ばねはどのような所で用いられているか?振動問題とは具体的にどのようなものがあるのか? A6-1 防振ゴムは,比較的周波数が高く,変位が小さい振動の低減に適している。 安価で取り扱いも用意であることから,ポンプ,送風機,エンジン,発電機, 電動機,圧縮機,など広範囲にわたって使用されている。 空気バネは,防振ゴムに比べて周波数が低く,変位が大きい振動の低減や 微振動の低減に適している。プレス機,新幹線,床全体の防振や,精密機器 を微振動から守る除振装置などに使用されている。 Q6-2 振動問題とは具体的にどのようなものがあるのか? A6-2 防振や制振が必要となる振動問題のいくつかの例を以下に挙げる。 電車や自動車 ・レール面(道路)の不整によって発生する車体の振動 ・高速走行に伴って発生する自励振動 ・パンタグラフの自励振動 ・エンジンの回転によって発生する車体の振動 機械類 ・プレス機械の衝撃による床振動 ・コンプレッサのピストンの運動による床振動 建築物 ・風や地震によって発生する橋桁や橋のケーブルの振動 ・風や地震によって発生する高層ビルの振動 ・風による送電線の振動 Q6-3 他にアクティブ制振装置はどのような場面で用いられるか? A6-3 アクティブ制振装置といっても,動吸振器型だけではない。空気圧,電磁石, 圧電素子,磁歪アクチュエータなどといったアクチュエータを用いて,制振対象の振動に 応じて制御力を発揮し,制振する方法も数多く実用化されている。 アクティブ制振装置が利用されるのは,制振対象の振動特性が時間的に変化する場合, ランダムな加振を受ける場合,非常に小さな振動を低減したい場合などである。 乗り物では,主に乗り心地の向上を目的として,電車,エレベータ,船などに 用いられている。 半導体製造装置など微振動を嫌う機械には,アクチュエータを利用した除振装置と呼ばれる 微振動低減装置が適用されている。 建築物では,超高層ビル以外にも,建設の進捗に伴って振動特性が変化する橋のタワーなど にはアクティブ動吸振器が使用されている。 Q7-1 振動が非線形であるか線形であるかの違いで、ゆれの感じ方に違いは生まれるのか? A7-1 非線形振動の場合には、主共振以外に2次共振が発生する。また、跳躍現象により入力周波数が変化すると揺れ方が急激に変化する場合がある。 Q7-2 シートにガタがない場合は、どのような振動になるのか? A7-2 共振点が高周波数側に移動し、バックスラップが生じ、低周波数領域での揺動感がなくなる。 Q7-3 ウレタンフォームの伝達関数の設定時に、不快振動の循環はどのように考慮されているのか? A7-3 不快振動が入力される周波数帯のゲインが下がるように伝達関数を設定する。ばね定数で共振点を設計し、減衰比でゲインを設計する。 Q7-4 この変位-荷重特性からはばね定数をどのように求めるのか? A7-4 下図に示すように、変位−荷重特性と振動時の相対変位より得られる直線(1)、(2)、(3) の傾きより求める方法があり、(1)で得られたばね定数がよく一致する。 
Q7-5 ヒステリシス損と減衰力は同じものなのか? A7-5 ヒステリシス損と減衰力は違うものである。ヒステリシス損は、系の状態を循環的に変化させたときに主に固体摩擦、内部減衰などによって失われるエネルギー量を表す。一方、機械振動においてその自由振動を時間と共に減少させる効果を生み出す作用を減衰と呼び、この作用が振動する質量に及ぼす抵抗力を減衰力と呼ぶ。減衰を生み出すメカニズムには、粘性力によるもの、摩擦によるもの、磁気力によるもの、電磁気力によるもの、材料弾塑性力によるものがあり、これらの生み出す減衰力には、振動の速度に比例するもののみならず、振動の変位や速度の非線形関数になっているものもある。 Q7-6 ランダム振動入力とは、具体的にはどのようなことをすることなのか? A7-6 この例におけるランダム入力振動とは、実車で道路上を走行して採取した加速度パワースペクトル値と等価な入力振動を動電型加振機により再現した励振波形のことをいう。 Q7-7 単一の調和励振とはどのようなものなのか? A7-7 単一周波数で変位が時間に対して正弦または余弦関数状に変化する周期運動を単一の調和振動と呼び、外力による励振が調和振動で表される場合を調和励振と呼ぶ。 Q7-8 相対変位とは、何と何の相対変位なのか? A7-8 外力による入力変位と振動モデルの出力変位の相対変位のことを示す。 Q7-9 線形ばねにおいて、具体的にどういった場面で重ね合わせの原理が使われるのか? A7-9 個別の要因に対する応答を求めておき、これらを加え合わせることにより、いくつかの要因に対する系の応答を求めるのに使う。 Q7-10 硬化ばね、軟化ばねにはどんなものがあるのか? A7-10 大型トラックや貨物車の緩衝用重ね板ばねで空車の場合と満車の場合いずれも良好な振動特性を与えるように設計したばねに硬化ばねを利用した例がある。軟化ばねには、ダイヤグラム式空気ばねで作ることもある。 Q7-11 磁石ばねはどのようなところで使われているのか? A7-11 実用化された例としては、高規格救急車用防振架台とトラック用サスペンションシートがある。 Q7-12 (b)、(c)、(d)の共振は、どのような場合に発生するのか? A7-12 A9-13・14、15、16を参照。 Q7-13 この磁石ばねに限らず、ばね力がf(x)=k1x+k2x2で表されるばねには1/2次分数調波共振が発生するのか? A7-13 分数調波共振は、減衰が小さい場合、ばねの種類に関係なく発生する。 Q8-1 風による送電線の振動では、負性抵抗がどのように働いているか? A8-1 送電線が上方に揺れているときには、風は相対的に斜め上方からあたることになる。その結果、運動と同じ方向に揚力が作用し、運動を助長させる。この変動揚力は、送電線の速度に比例した力で、これが負性抵抗として作用する。 Q8-2 チョークの振動ではどのようにモード連成が起こっているのか? A8-2 チョークの振動では、チョークを引きずる方向に並進振動の自由度を持ち、チョークを持つ手の指先を回転中心とした回転振動の自由度を持っている。この2つの自由度の間で連成作用が発生している。 Q8-3 自由振動と強制振動の違いは何か? A8-3 自由振動とは、初期状態として変位や速度を与え、その後は何の力も作用させない状態を続けた時の振動挙動を指し、強制振動とは、初期状態で変位や速度を与えた後も引き続いて力を与え続けた時の振動挙動を指す。 Q8-4 並進ギャロッピングを防ぐ方法はあるのか? A8-4 構造側からの対応としては構造減衰を増やすことが一般的に行なわれる。また、空気力学的対応としては、並進ギャロッピングを発生させないような流体力特性を持った形状に変更することが行なわれる。 Q8-5 渦励振を防ぐための工夫にはどのようなものがあるのか? A8-5 規則的な渦放出を阻止することができれば渦励振は防げるので、構造物の形状を非一様にすること(テーパ形状にしたり、段付きにすること)が効果的である。 Q8-6 スロッシングとはどのようなものか? A8-6 スロッシングとは、自由表面を持つ容器内に満たされた液体の振動現象のことで、重力が復元力となっている液面揺動のことを指す。 Q9-1 往復動機関と速度形機関はどう違うのか? A9-1 往復動機関は、シリンダの中でピストンを往復運動させることにより、燃焼ガスの静圧を利用して仕事を行う静圧形機関をいう。速度形機関は、作業ガスを膨張させ、保有する内部エネルギーを高速噴流の運動エネルギーに変換した上で仕事を行う動圧形機関のことをいう。 Q9-2 往復運動と回転運動間の変換機構には、この他にどんなものがあるのか? A9-2 ピストン・クランク機構は、機構学では往復すべりこクランク機構と呼ばれている。ここでは、機構学でよく知られている主な変換機構の例を以下に示す。
Q9-3 連接棒の最大慣性モーメントと、それを生じるθの値を出すことはどのような意味をもつのか? A9-3 連接棒は往復運動を行う部分と回転運動を行う部分を持ち、往復運動のみを行うピストンや回転運動のみ行うクランクと比較して複雑な運動を行うため、連接棒の運動の理解を助けるために示した。クランク回転力の反作用と連接棒の慣性力は、機関の支持台への影響が大きく、設計上重要なポイントになる。 Q9-4 ここで、ピストンに加わる慣性力は考慮したのに、連接棒に加わる慣性力は考慮しなかったのはなぜか? A9-4 連接棒に加わる慣性力は直接式の中には表れない。これは、ピストン・クランク機構のダイナミックスを理解しやすくするためである。ピストンの慣性力については次の画面5で説明している。 Q9-5 大きな慣性モーメントを持つはずみ車とはどのようなものか? A9-5 画面8にて得られる慣性モーメントIが大きい場合となる。具体的にはリム、スポーク及びボス重量の大きいもの、リム中心線半径の長いものとなる。 Q9-6 エネルギーの吸収または放出はどうして起こるのか? A9-6 原動機は1サイクル中あるいは、各瞬間ごとに出力が大きく変動し、回転トルクと抵抗回転トルクの間には常に差があり、変動している。そのため回転速度を一定に保つためにはエネルギーを吸収または放出する必要が生じる。この大きな運動エネルギー(慣性モーメント)を持つ回転板がはずみ車である。 Q9-7 角速度変化量と慣性モーメントの関係式はどのようにして出てきたのか? A9-7 機関回転運動部分を回転軸に関する慣性モーメントIである円板と考え、これが角速度ωで回転するとき、クランク回転力Cおよび抵抗回転力CRが働いているものとすると、運動方程式は  で表される。 で表される。ある定常状態では角速度 Q9-8 なぜはずみ車の慣性モーメントはΔE1から得られるのか?ΔE2やΔE3ではだめなのか? A9-8 機械の作業エネルギーに対して、原動機の出力エネルギーが過不足することによって生ずるクランク回転速度の変化は、はずみ車の慣性モーメントIに反比例する。そのため、クランク回転トルク曲線と平均抵抗回転トルク曲線で囲む面積のうち、最大面積で表されるエネルギーΔE1を当てている。 Q9-9 mc、mrp、mrcがこのように表せる理由は何か? A9-9 連接棒の場合、質量mrを2分割して質量mrp、mrcなる2質点系に置き換え、その力学的特性をmrp、mrcが質量のない剛性だけを持つ1本の棒でつながれた質点系の力学的特性と等価であるとすることができる。クランクの場合は、クランクピン質量とクランクアーム質量及びその重心のクランク軸中心からの距離による遠心力を、クランク軸中心からのクランクピンの距離とクランクピンの位置にある等価質量による遠心力が等しいとしている。 Q9-10 慣性力を1次慣性力、2次慣性力と分けることは、どのような意味があるのか? A9-10 高次のハーモニック成分が含まれると完全なつり合わせはできません。この場合、例えば、単気筒機関の場合は、2次慣性力をつり合わせるためには2θで回転する別の機構を取り入れることが必要があり、1次成分のみの減少を図ることがある。多気筒機関の場合、不つり合い力及び不つり合いモーメントを各々別々に重ね合わせたものになる。往復部質量のつり合わせは、1次慣性力をつり合わせることが最も重要で、ついで2次慣性力のつり合わせを考える。慣性力及び慣性モーメントのつり合わせは1次慣性力と2次慣性力で仮想回転質量と角速度、クランク角が異なる。そのため、1次慣性力、2次慣性力と分けて考えることが必要になる。 Q9-11 多気筒の場合、回転質量を0にすることは可能か? A9-11 単気筒機関の回転部質量による慣性力は遠心力で、これはクランクと反対方向につり合い錘を取り付けることによってつり合わすことができる。単気筒機関の回転部質量をつり合わせることができるので多気筒機関の回転部質量もつり合わせることができる。ところが多気筒機関は各気筒ごとに慣性力と慣性モーメントが作用するので機関支持台には合成したものが作用する。この場合、つり合い錘を各クランク毎に取り付ける必要がないのみならず、つり合い錘を取り付けなくてもつり合っていることがある。 Q9-12 回転部質量に対するつりあい錘と往復部質量に対するつりあい錘は同じものなのか? A9-12 回転部質量に対するつり合いと往復部質量に対するつり合いを求め、これらを加え合わせることにより、これら二つの要因に対するつり合いを求めたものである。そのため、回転部質量と往復部質量に対するつり合い錘は、それぞれの慣性力をつり合わせるためには、それぞれのつり合い錘が必要となる。 Q9-13 実際は、過分つりあわせと部分つりあわせのどちらがより使われているのか? A9-13 過分つり合わせは、1次慣性力のx成分がなくなる代わりにy成分が生じる。つまり、慣性力の向きが変わるだけで慣性力が除かれたわけではないため、1次慣性力のx成分とy成分の振幅の大きさが等しくなるように調整される部分つり合わせがより使われる。 Q9-14 なぜ多気筒小容量機関を使えば大馬力を作ることができるのか? A9-14 エンジン回転数を上昇させても、出力は逆に低下する傾向にある。すなわち、高速回転により高出力を得るには、高速回転でもエンジンの吸い込み能力を低下させないように吸排気速度を低下させる必要がある。吸気流速は気筒数の3乗根に逆比例し、多気筒化するほど同一回転数での吸気流速は低下する。そこで、吸気流速が低下した分だけ、多気筒エンジンは、高回転化が可能となり、同一行程容積で高出力が得られることになる。 Q10-1 軸受から受ける力、回転体に作用する不安定化力、熱応力の中で特に注意するものは何か? A10-1 対象となる機器によって重要なものは変わってくる。例えば、すべり軸受で支えられているエンジンでは軸受からの力、ポンプなどの流体機械では隙間部分を流れる流体から受ける不安定化力、蒸気タービンなどでは熱応力が重要となってくる。 Q10-2 減衰器を除いたモデルで考えても、実際の動きとの違いは生じないか? A10-2 減衰器を除いたモデルでは実際の動きよりは振幅は小さくなる。特に共振点近傍での振幅は違ってくる。しかしながら、設計にあたって重要な共振点の位置など共振特性の大域的な検討はこのモデルで行なうことができる。 Q10-3 材料力学の公式とはどのようなものか? A10-3 両端単純支持はりの特定の場所に荷重が作用したときに発生する任意点でのたわみを与える公式のこと。教科書や便覧にも掲載されている。 Q10-4 コマのこのような性質はなぜ生まれるのか? A10-4 角運動量保存則の性質によって理解することができる。詳しくは、力学と運動の基礎のレッスンに戻って学習すること。 Q11-1 ひとつひとつの部品を分けて考えることは当たり前のような気がするが、部品をまとめて扱うこともあるのか? A11-1 自動車のコーナリング運動や人工衛星の軌跡計算などのように、広い範囲にわたる運動を考える場合に、すべての部品をまとめて1つの剛体として取り扱うことがある。しかしながら、これは簡略化された取り扱いであるため、計算は容易になるが、精度という点では不十分な場合もある。 Q11-2 マルチボディシステムとは何か? A11-2 複数の部品によって構成され、それぞれの部品が相対的に運動するシステムは全てマルチボディシステムということができる。 Q11-3 一般化座標が独立とはどういうことか? A11-3 拘束条件式は、いくつかの一般化座標の間において成立する関係を記述したものになる。このとき、拘束条件式に現れる一般化座標は、互いに従属な関係にある、あるいは、互いに独立ではないと表現される。 Q11-4 時間tが拘束条件に含まれるものにはどんなものがあるか? A11-4 クイックリターン機構で説明したモータのように、回転速度が一定である要素の場合、回転角θはαを比例定数として次のように表すことができる。 θ(t) = α×t また、回転速度が一定ではなく、時間の関数で表される場合も、時間tが拘束条件に含まれる。 Q11-5 拘束条件を微分したものが拘束条件式を一般化座標で偏微分したものと一般化座標の微分の積となるのはなぜか? A11-5 偏微分と全微分の間に成立する基本的な関係式である。大学教養課程の数学で学習する。 Q11-6 m>nとなることはないのか? A11-6 m>nとなる場合、すなわち拘束条件の次数が運動方程式の次数より大きくなることはない。 Q11-7 ここではθを独立一般化座標としましたがxやyを独立一般化座標としてもよいか? A11-7 よい。ただし、xやyを独立一般化座標とした場合、得られる解は複雑な形になる。 Q12-1 調和振動とは何か? A12-2 「機械工学辞典を参照のこと。」 Q12-3 Cの任意の値でよいのか? A12-3 Cの値は任意で構わないが、C=1とおくと基準関数の振幅が1となる。これによってAiとBiが物理的に意味を持った振幅となるため、直感的な理解が容易になる。この様な理由から、本学習ではC=1としている。 Q12-4 AiとBiも無限個存在するのか? A12-4 iは連続体の振動をモードごとに分解したときの次数を表している。したがって、i次モードの振幅を表す定数であるAi及びBiは、モードの数だけ無限個存在する。 Q12-5 有意なモードはどのくらいあるのか? A12-5 有意なモードとは、対象としている連続体の振動を記述する場合に無視することのできない重要な振動モードを意味する。 たとえば、風で揺れる高層ビルや橋のケーブルは、主に1次や2次といった低次の振動モードで振動し、高次のモードになるほど揺れにくいという特徴を持っている。このような場合には、3次や4次程度のモードまで考慮すれば、その振動現象を把握する上では十分である。 しかし、比較的高い周波数成分を持った地震で高層ビルが加振される場合、その周波数成分に対応した振動モードまでを考慮する必要がある。さらに、この高層ビルにアクティブ制振装置を設置する場合などは、高次モードを不用意に無視してしまうと「スピルオーバ」と呼ばれる現象が発生し、かえって構造物に悪影響を与えてしまうおそれがあるため、注意が必要である。 つまり、同じ連続体でも外力の種類などによって、有意なモードの捉え方が異なるため、現象を十分に理解して解析することが重要である。 |