そこで実際に、この結果を考慮して、予め用意するお釣りの量を決定します。
このとき例えば、「結果の平均」より用意するお釣りを決めるのであれば、−6となり、5千円札6枚用意すればよいと判断することになります。
一方、平均値では不安だと考える人もいるでしょう。その場合は、シミュレーションにより得られた結果の最小値を選ぶという方法も考えらます。その場合は、最小値−10(7回目の結果)より、5千円札を10用意することになります。
それ以外にも、シミュレーション結果のうち、何割かをカバーできればよいという考え方もあります。例えば、予め8枚の5千円札を用意しておけば、上で行った10回のシミュレーション実験のうち9回はお釣りが不足しないのだから、実際にも、9割程度の確率でお釣りの不足はなさそうだ、と考える人もいるでしょう。
また、シミュレーション結果の最小値よりも少なくなることを警戒する場合は、10枚プラスαの枚数を用意することも考えられます。
このように、シミュレーションにより得られた結果をどのように扱うかに関しても、最終的には意思決定者が、状況などを加味した上で判断する必要があります。

Q11
「所持金が5,000円でも、貨幣では払わない」とはどういう意味ですか?
A11
今回の例題では、所持金の下4桁が5,000円以上の場合はお釣りが不要な支払い方をすると仮定しています。しかし、これはモデル化のための簡略化であって、実際に所持金の下4桁が5,000円であっても、例えば千円札4枚と貨幣1000円分という場合もあり得ます。
このような場合、現実的には1万円札で支払われるでしょう。これが、「所持金が5,000円でも、貨幣では払わない」という意味です。
もし、このような点まで考慮したい場合は、採用したモデルを再考する必要があるでしょう。

Q12
制約条件や評価関数が1次式で無い場合は、どのように最適解を求めるのですか?
A12
例えば、制約条件が1次式で評価関数が2次式の場合は2次計画問題と呼ばれ、専用の解法が存在します。ただし、制約条件や評価関数がそのように限定される場合ばかりではありません。そのような場合は、制約条件や評価関数の勾配(微係数)情報を用いて近似的な問題を考え、繰り返し計算により最適解を求めることが行われます。
このような手法では計算量が膨大になりますが、近年のコンピュータの発達により、普通のパソコンでも計算を実行することが可能になってきています。

Q13
数式で表現できない最適化問題もあると思いますが、そのような問題にはどのようにアプローチするのですか?
A13
複数の選択肢から最適な選択を見つけるための組み合わせ最適化問題などが、数式での表現が難しいものの代表です。このようなものには、一つ一つの選択肢を生物の遺伝子に見立てて進化の過程を模したモデルで最適解を見つける方法である遺伝的アルゴリズム(GA)や、神経回路網を模したニューラルネットワーク(NN)などのアプローチが存在します。
いずれもコンピュータの発達を前提とした手法といえます。

Q14
最適化手法は、政策の決定や企業の経営にも使えるものなのですか?
A14
政策決定や企業経営は単純な数式などで表現することが難しいため、そのまま適用できるものではありません。最適化手法の問題というよりは、モデル化の問題ということが出来ます。
ただし、意思決定論という分野もあり、階層分析法(Analytic Hierarchy Process ; AHP)といった手法や経済学から発展したゲーム理論を適用する手法などが研究されています。

Q15
最適化手法に特許が与えられたというのは本当ですか?
A15
線形計画問題の解法であるカーマーカー法(内点法の一種)の特許が日本でも1996年に設定登録されています。数学の特許認定は学問の発展を阻害するという意見も多く、議論を呼んでいます。

Q16
線形計画問題では、どのぐらいの変数の数を扱えるのですか?
A16
アルゴリズムに関する理論的な制約はありません。純粋にコンピュータの能力ということになります。現在(2003年)であれば、パソコンでも数万や数十万の変数を扱うことが可能です。

Q17
「環境保全コスト」が1,400万円で、「環境保全対策に伴う経済効果」が10万円ならば、1,390万円の赤字となるのですか?
A17
企業は、環境保全活動を独立して業務としているわけではありません。つまり、環境保全活動だけで採算を取ろうとしているわけではないのですから、「環境保全コスト」と「環境保全対策に伴う経済効果」のように貨幣単位で比較できる部分だけを対比して、黒字か赤字かを議論することには意味がありません。
環境会計は「会計」という名前こそ付いていますが、金額数値だけで完結するものではなく、二酸化炭素排出量や廃棄物排出量の削減量のような物量数値、さらに、環境保全活動が環境上のリスクの低減に貢献しているような場合の定性的記述なども含めた、総合的な計算体系と理解すべきものなのです。

Q18
どうして、成功確率を1と考えてよいのですか?
A18
まず、ETの定量化を行う際の各分岐点における失敗確率とは、故障(動作不良)している時間を大まかに捉えるための値であるということがポイントです。
つまり、失敗確率とは、ある機器の故障が、例えば10年に1日間程度故障しているのか、100年に1日間程度故障しているのか、ということを大凡で捉えるための値に過ぎません。また失敗確率は、一般的に非常に小さい値となります。
これらを踏まえて、次のようなイベントツリーを考えてみます。
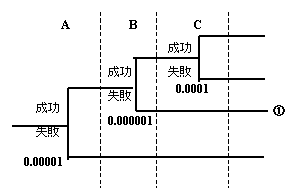
3つの分岐条件A,B,Cにおいて失敗する確率を、それぞれ、0.00001、0.000001、0.0001とすると、このときの各点の成功確率は、それぞれ、0.99999、0.999999、0.9999となります。
(「"成功確率"=1−"失敗確率"」より)
例として、「点Aでは成功、点Bで失敗」する場合(図中の(1))の確率は、
0.99999(Aの成功確率) × 0.000001(Bの失敗確率)=0.00000099999
となります。
一方、点Aで成功する確率を1とした場合には、
1(Aの成功確率) × 0.000001(Bの失敗確率)=0.000001
となります。
これら2つの確率の差は、
0.000001 − 0.00000099999 = 0.00000000001 と求められます。
これは、点Bにおいて失敗する確率(0.000001)に比べて十分に小さいため、故障の確率を捉えるという意味では、無視してよい差であると考えられます。またこのことは、ツリーの他の点についても当てはまります。
以上のような理由により、各点の成功確率を1と見なしてもよいと考えられるのです。
Q19
どうして、失敗する確率の大部分がPSとPBといえるのですか?
A19
レッスン中で作成したETより、仮想系の分室が浸水してしまうシナリオと、各シナリオの失敗確率は次のように求められました。
説明を簡単にするため、ETの各分岐点における失敗確率PS
,PB ,PP,PA ,POは、それぞれ同じ程度に小さい値をもつものとします。
いま仮に、それらが全て0.00001と仮定した場合、各シナリオの失敗確率は以下のようになります。
このとき、最終的に仮想系の分室が浸水する全確率は、(1)〜(4)を足したものですから、
(1)+(2)+(3)+(4)=0.0000200002となります。
その中における(1)と(2)の占める割合を計算すると、 (0.00001 + 0.00001)/
0.0000200002 ≒ 0.99999となるため、最終的に分室が浸水する場合の99.999%は、PSかPBの故障に起因することになるのです。
このような分析を行うことにより、PSやPBを小さくすることが、最終的な失敗確率を小さくするために効果的であることが導き出せるのです。

Q20
機器の失敗率はどのようにして求めるのですか?
A20
失敗確率の算出方法は非常に複雑な問題であるため、ここでは、求め方の基本的な考え方を説明しましょう。
ある機器の導入時点から故障するまでの平均時間をA、その機器が故障してから修理または交換が完了するまでに要する平均時間をBとすると、
失敗確率 = B/(A+B)
で求められます。この値をアンアベイラビリティといいます。つまりこの値は、機器が使用できない状態(故障が発生し、修理や交換が完了して再び利用可能になる時点まで)が発生している時間の割合です。
理論的にはこのようにして求められますが、現実にこれを各機器について計算することは、様々な難題があり、決して容易であるとはいえません。
なお、原子力施設や化学プラント施設等で利用される主な機器に関しては、故障確率を収集したデータベースが存在しており、それを用いてET分析等を行う場合もあります。

Q21
自然保護や緑化等のコストは、社会活動コストではなく管理活動コストに区別されるという考え方もあると聞いたのですが?
A21
確かに管理活動コストに区別される場合もあります。
その基準に関しては、自然保護や緑化を行う場所によって区別されているのではなく、実際の事業活動の範囲かどうかという視点による区別を想定しています。従って、実際の事業活動の範囲にあるものについては管理活動コストに含め、事業活動とは直接関係ない範囲については社会活動コストに含めます。
例えば、砂漠化防止のためにボランタリーに緑化を行う場合は、社会活動コストに該当します。また、自社の所有地において森林を育成している場合は、基本的には管理活動コストですが、それが社会に解放された取り組みであれば、自社敷地内であっても社会活動コストに該当すると考えられます。

Q22
環境会計に記載すべき情報のうち、物量や金額で表せないものはどうすればよいですか?
A22
環境会計は環境保全活動の状況を定量的に捉える仕組みですが、環境省のガイドラインでは、定量的情報による集計結果の他にも、定性的情報を積極的に盛り込むべきであるとしています。
環境会計の構成要素ごとに貨幣単位あるいは物量単位で測定することとしていますが、物量や金額で表せないものについては、定性的情報によって記述することが可能です。
また、環境会計において基本となる重要な事項や集計結果に対する説明なども、定性的情報に区分されます。
| |
|
構成要素
|
定量的情報
|
定性的情報
|
|
環境保全コスト
|
貨幣単位
|
取り組みの内容
|
|
環境保全効果
|
物量単位
|
効果の内容
|
|
環境保全対策に伴う経済効果
|
貨幣単位
|
効果の内容
|
|

Q23
環境保全コストに入るかどうかの判断基準について教えてください。
A23
環境保全コストに該当するかどうかの判断の基準として、環境保全を目的として支出したコストであるかどうかに基づく基準(目的基準)のほかに、目的としなくても結果的に環境保全効果のある支出であったかどうかに基づく基準(効果基準)という考え方があります。
環境省のガイドラインでは、原則として目的基準のみを採用していますが、この理由は、環境保全対策と環境保全の効果との因果関係を考えた場合に、目的基準により環境保全対策活動に要したコストを集計する方が、効果から環境保全対策へ遡るより合理的だからです。
また、効果基準によりコストを把握することは、経営上の意思決定への有効性に欠けること、結果的に環境保全効果のあったコストを特定することは容易でないこと、目的基準のみによる企業との比較可能性が損なわれること、などの理由により、必ずしも適切でないと考えられます。
 Q24
Q24
従来品より価格が低い商品のグリーン購入の場合、追加的コストをどうすればよいですか
A24
グリーン購入した環境物品が、環境に配慮されていない一般の物品と比べて価格が低い(購入のための追加的コストがマイナスになる)場合も考えられます。
この場合は、該当する財・サービスが環境保全対策として一般化していることを意味しており、この場合は、環境保全コストが発生していないものとみなします。
しかし、追加的コストがマイナスとなる場合でも、該当する財・サービスが環境保全対策として一般化していないことが明らかな場合は、環境保全対策に伴う経済効果に該当します。
従来の資材より安価になる例として、部材等を環境に配慮した独自仕様に設計変更して調達する場合は、環境保全対策に伴う経済効果とすることが適当です
。

Q25
環境会計の集計結果に対する説明について、教えてください。
A25
環境保全への取り組みを環境会計によって定量的に把握した結果を、経営者等自らが分析・評価します。これにより、企業等の現在の状況や将来の方向性がより明確になり、情報の利用者の理解を容易にするのに有効です。
なお、このような手法は企業財務の情報開示においても、経営者による討議と分析(Management's
Discussion and Analysis
)として、有効な開示項目となっています。

Q26
トラベルコスト法とはどのような手法ですか。
A26
トラベルコスト法は、その名の通り、人々がある環境を訪問する際に要する交通費などから、その環境の価値を算出する手法です。人々は、その環境に大きな価値があると判断した場合、多くの時間や費用をかけてでも、そこへ行こうとします。トラベルコスト法は、人々のこういった支出を評価に利用し環境の価値を算出する手法です。
トラベルコスト法において、人々の環境に対する間接的な消費の調査は、主に面接によって行われます。面接調査の内容は、移動の費用、例えば公園などの環境で出費する金額、移動に要する時間などです。これらの項目から、訪れる人々の平均的な総費用を計算します。移動に要する時間も、ここでは金額に換算することで考慮されます。
また、年間訪問回数や訪問する人々の所得なども調査項目になります。ここから、平均的な訪問者の姿を想定することになります。
これらの調査によって、平均的な訪問者の支払意志額が算出されることになるので、この意志額に基づき、環境の価値を算出します。

Q27
ヘドニック価格法とはどのような手法ですか。
A27
ヘドニック価格法は、環境に関する要素を含んだ財に与えられている値段をもとに、その環境についての評価を分析する手法です。例えば、良い環境にある住宅は、値段も高くなるはずです。ですから、その近くにある環境施設は、同じく良い環境にあると推測できます。ヘドニック価格法では、このような環境に関連する財の価格を用いて、対象となる環境を評価します。
住宅の位置や特性、住環境などの要素が関連して、住宅の値段が算出されていると仮定します。ヘドニック価格法では、こういった要素に基づいて、住宅の価値を導くための算出式(ヘドニック価格関数)を定義することで環境の価値を算出します。

Q28
仮想評価法の手順の流れについて、もう少し詳細に教えてください。
A28
仮想評価法の流れを以下に示します。
・最初に、評価対象を決定します。ここでは、対象となる環境そのものの範囲や環境から影響を受ける人々の範囲が決められます。
・次に、情報収集と事前調査を行います。
・また、対象となる人々の環境への関心についても情報が必要で、10人程度のグループインタビューを行うこともあります。
・仕入れた情報を元に調査票を作成し、プレテストを行います。プレテストは、調査票のチェックとして実施されます。
・本調査では、準備した調査票に基づいて、面接・電話・郵送などの方法で調査が行われ ます。
・本調査の結果を集計すると、個人評価額が得られます。
・最終的に、個人評価額と対象人数から環境そのものの貨幣評価を導きます。個人評価額と対象人数を掛け合わせた値を環境の価値とすることが一般的です。

Q29
仮想評価法とコンジョイント分析のどちらが有効な手法なのですか。
A29
仮想評価法は、コンジョイント分析よりも昔から用いられており、事例も多数あります。ですから、包括的に評価したい場合には有効です。しかし、環境を構成する属性を詳細に見たい場合は、仮想評価法よりコンジョイント分析が良いでしょう。とは言え、コンジョイント分析も、考慮すべき属性が抜け落ちていないかどうか、注意が必要です。
ですから、どちらが有効というわけではなく、目的に応じて手法を選び、適切な方法で試算することが大切です。

Q30
コンジョイント分析の種類について教えてください。
A30
コンジョイント分析には、選択型、ランキング型、ペアワイズ型などがあります。
選択型コンジョイントは、提示する一覧の中から、アンケート被験者にとって一番良いと思うものを選んでもらう方法です。
ランキング型は、一覧の中に示す行動について、それぞれ順位をつけてもらう方法です。
ペアワイズ型は、二つの行動のペアを表示して、どちらがどれだけ望ましいかについて評点をつけてもらう方法です。
その他には、完全評点型コンジョイント、適応コンジョイント(ACA)などがあります。

Q31
ここで用いている評価式・連立方程式について詳しく教えて下さい。
A31
ここで用いている評価式はあくまで一例であり、以下に評価式を構成するa, b, c, d, v の値について説明します。
【a】
ここでa,b,cは「重み」と言っていますが、例えばaは、砂浜が再生されることにより人々が感じる正の効用(幸福感)を表現する値であり、同時にこの場合では砂浜の価値を意味しています。但し、この「砂浜の価値」は○○円といった経済的な価値を表しているわけではありません。この評価式における1000円の価値(c)を基準とした価値のため、「砂浜の経済的価値」はa/c×1000で表されることになります。
【b】
bもaと同様に、植林による正の効用及び価値を表す値です。
【c及びv】
cは1000円の価値そのものを表現していますが、logcとして人々が1000円の税金を支払う際の負の効用(コスト感)を表しています。一般的にはlogcではなく単なるcとする場合が多いですが、1000円の価値が0や負になることを防ぐためにlogcとしています。ここで1000円という数字は、単に基準となる値として任意に設定しています。
また、2000円の効用は2.0 logc、3000円の効用は3.0 logcというように仮定しています。この2.0や3.0などが評価式におけるvに相当します。
【d】
dは、このようなモデルを仮定する際に生じる定数項であり、モデル4では砂浜再生や植林などを行わないことを希望する人々の支持率を表現しています。
コンジョイント分析では、各属性の効用の総和により全体効用とする「ランダム効用モデル」が多く用いられています。評価式もランダム効用モデルを基本として構成されており、効用(a, b, -vlogc, d)の総和が全体効用(ここでは人々の支持率xを代用)を表しています。この評価式は、各モデルにより異なっています。例えばモデル2の式ではbの項がありませんが、これは「植林は実施しない」ために植林の効用bが含まれていないためです。

